BT Question Set P1-T2-20-23 set: ARMA process
Learning objectives
- Explain mean reversion and calculate a mean-reverting level.
- Define and describe the properties of autoregressive moving average (ARMA) processes.
- Describe the application of AR, MA and ARMA processes.
Let’s load some packages
library(tidyverse)## -- Attaching packages --------------------------------------------------------------------------------- tidyverse 1.3.0 --## v ggplot2 3.3.2 v purrr 0.3.4
## v tibble 3.0.3 v dplyr 1.0.2
## v tidyr 1.1.2 v stringr 1.4.0
## v readr 1.3.1 v forcats 0.5.0## -- Conflicts ------------------------------------------------------------------------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()library(forecast) # incl ggACF()## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo# library(cowplot)
library(patchwork)20.23.1. Below are plotted the autocorrelation function (ACF) and partial autocorrelation function (PACF) for a simulated time-series process. Please note that the horizontal dashed blue lines represent the 95.0% confidence interval … Which of the following time-series models is most likely described by these ACF and PACF plots?
set.seed(66)
AR_param_1 = 1.4
AR_param_2 = -0.7
AR_intercept = 0
AR_n <- 1000
theme_set(theme_bw())
# arima.sim model c(p, d, q)
# p = AR order
# d = difference
# q = MA order
# Generate an AR(2) with parameters, AR_param_1 and AR_param_2
AR <- arima.sim(model=list(order=c(2,0,0), ar = c(AR_param_1, AR_param_2)), n = AR_n, mean = AR_intercept)
p3 <- ggAcf(AR) +
geom_segment(size = 3) +
labs(
title = "autocorrelation function (ACF)"
) + theme(
plot.title = element_text(size = 12),
axis.title.x = element_blank(),
panel.grid = element_blank()
)
p4 <- ggPacf(AR) +
geom_segment(size = 3) +
labs(
title = "partial autocorrelation function (PACF)"
) + theme(
plot.title = element_text(size = 12),
panel.grid = element_blank()
)
# Please note plot is shrunk to 86% on copy/paste
p3 / p4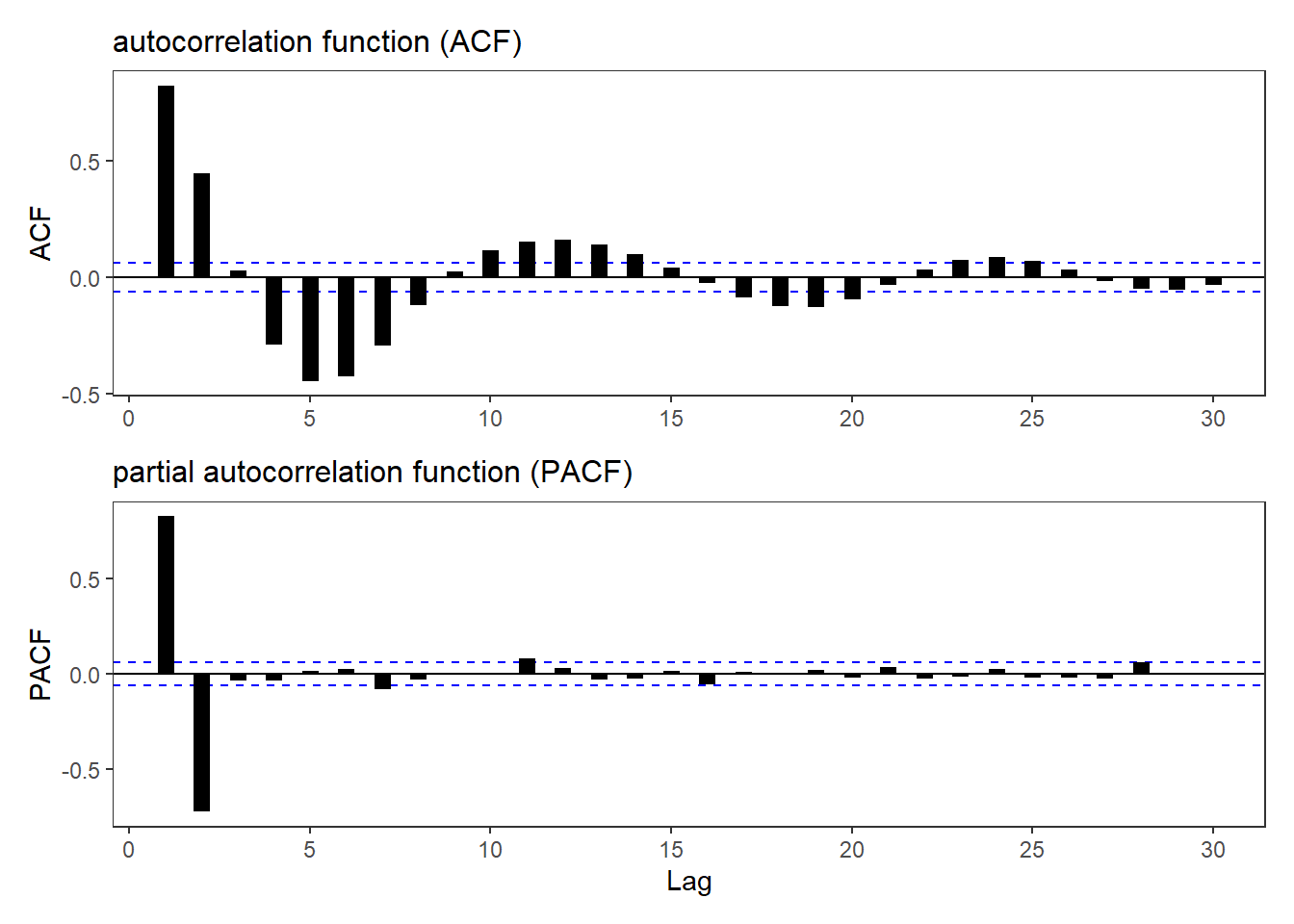
20.23.2. Below are plotted the autocorrelation function (ACF) and partial autocorrelation function (PACF) for a simulated time-series process. Please note that the horizontal dashed blue lines represent the 95.0% confidence interval … Which of the following time-series models is most likely described by these ACF and PACF plots?
set.seed(19)
MA_n = 1000
MA_mean = 0
MA_weight_1 = 0.4
MA_weight_2 = 0.6
MA_weight_3 = 0.8
# # Generate an MA(3) with weights MA_weight_1, MA_weight_2, and MA_weight_3
MA <- arima.sim(model=list(order = c(0,0,3), ma = c(MA_weight_1, MA_weight_2, MA_weight_3)), n = MA_n, mean = MA_mean)
p5 <- ggAcf(MA) +
geom_segment(size = 3) +
# geom_hline(yintercept = c(ci2, -ci2), color = "darkblue", linetype = "dashed", size = 2 ) +
labs(
title = "autocorrelation function (ACF)"
) + theme(
plot.title = element_text(size = 12),
axis.title.x = element_blank(),
panel.grid = element_blank()
)
p6 <- ggPacf(MA) +
geom_segment(size = 3) +
labs(
title = "partial autocorrelation function (PACF)"
) + theme(
plot.title = element_text(size = 12),
panel.grid = element_blank()
)
# Please note plot is shrunk to 86% on copy/paste
p5 / p6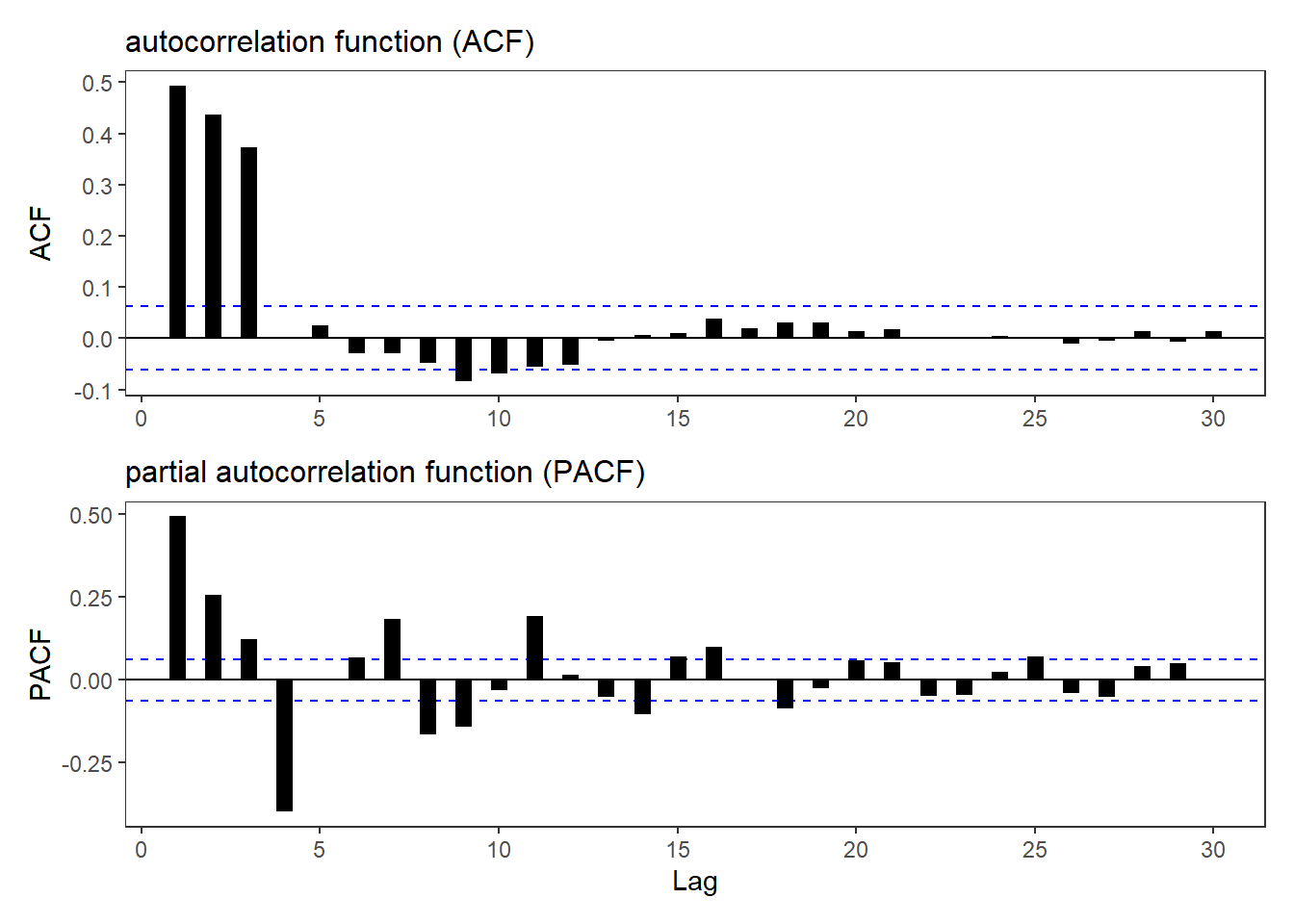
20.23.3. An ARMA(1,1) process evolves according to Y(t) = ẟ + ϕY(t-1) + θε(t-1) + ε(t). The plot below contains two 300-step ARMA(1,1) processes that differ only in their coefficients …
Which of the following statements is TRUE about the two ARMA(1,1) simulations above?
- Both of the ARMA(1,1) processes are likely to exhibit slow decay in both the ACF and PACF
- Both of the ARMA(1,1) processes are likely to cut off sharply at lag 1 in both the ACF and PACF
- The first ARMA(1,1) process (i.e., plotted with a red dashed line) cannot be covariance-stationary
- The unconditional mean of both ARMA(1,1) processes must be zero because all ARMA(1,1) have a long-run mean of zero
library(astsa)##
## Attaching package: 'astsa'## The following object is masked from 'package:forecast':
##
## gasset.seed(9)
ar_11_1 = 0.8
ma_11_1 = 0.6
arma_11_1_mu = 2
sim_n = 300
ar_11_2 = 0.9
ma_11_2 = -0.5
arma_11_2_mu = -3
# ar_22 = c(1.4, -0.6)
# ma_22 = c(0.9, 0.6)
ARMA_11_1 <- arima.sim(model=list(order = c(1, 0, 1), ar = ar_11_1, ma = ma_11_1), n = sim_n) + arma_11_1_mu
ARMA_11_2 <- arima.sim(model=list(order = c(1, 0, 1), ar = ar_11_2, ma = ma_11_2), n = sim_n) + arma_11_2_mu
# ARMA_22 <- arima.sim(model=list(order = c(2, 0, 2), ar = ar_22, ma = ma_22), n = 200)
# ts.plot(ARMA_11, ARMA_22)
time_arma <- bind_cols(ARMA_11_1, ARMA_11_2) %>% rowid_to_column() %>%
rename(y_ARMA_11_1 = ...1, y_ARMA_11_2 = ...2)## New names:
## * NA -> ...1
## * NA -> ...2theme_set(theme_bw())
colors <- c("First ARMA(1,1)" = "darkred", "Second ARMA(1,1)" = "steelblue")
time_arma %>% ggplot(aes(x = rowid)) +
geom_line(aes(y = y_ARMA_11_1, color = "First ARMA(1,1)"), size = 1, linetype = "longdash") +
geom_line(aes(y = y_ARMA_11_2, color = "Second ARMA(1,1)"), size = 1) +
scale_y_continuous(labels = scales::number_format(accuracy = 0.1)) +
theme(
axis.title.y = element_blank(),
axis.title.x = element_blank(),
axis.text.x = element_text(size = 12, face = "bold"),
axis.text.y = element_text(size = 12, face = "bold"),
legend.position = "right",
legend.text = element_text(size = 12)
) + labs(
title = "Two different ARMA(1,1) time-series simulations",
color = "Legend"
) +
scale_color_manual(values = colors)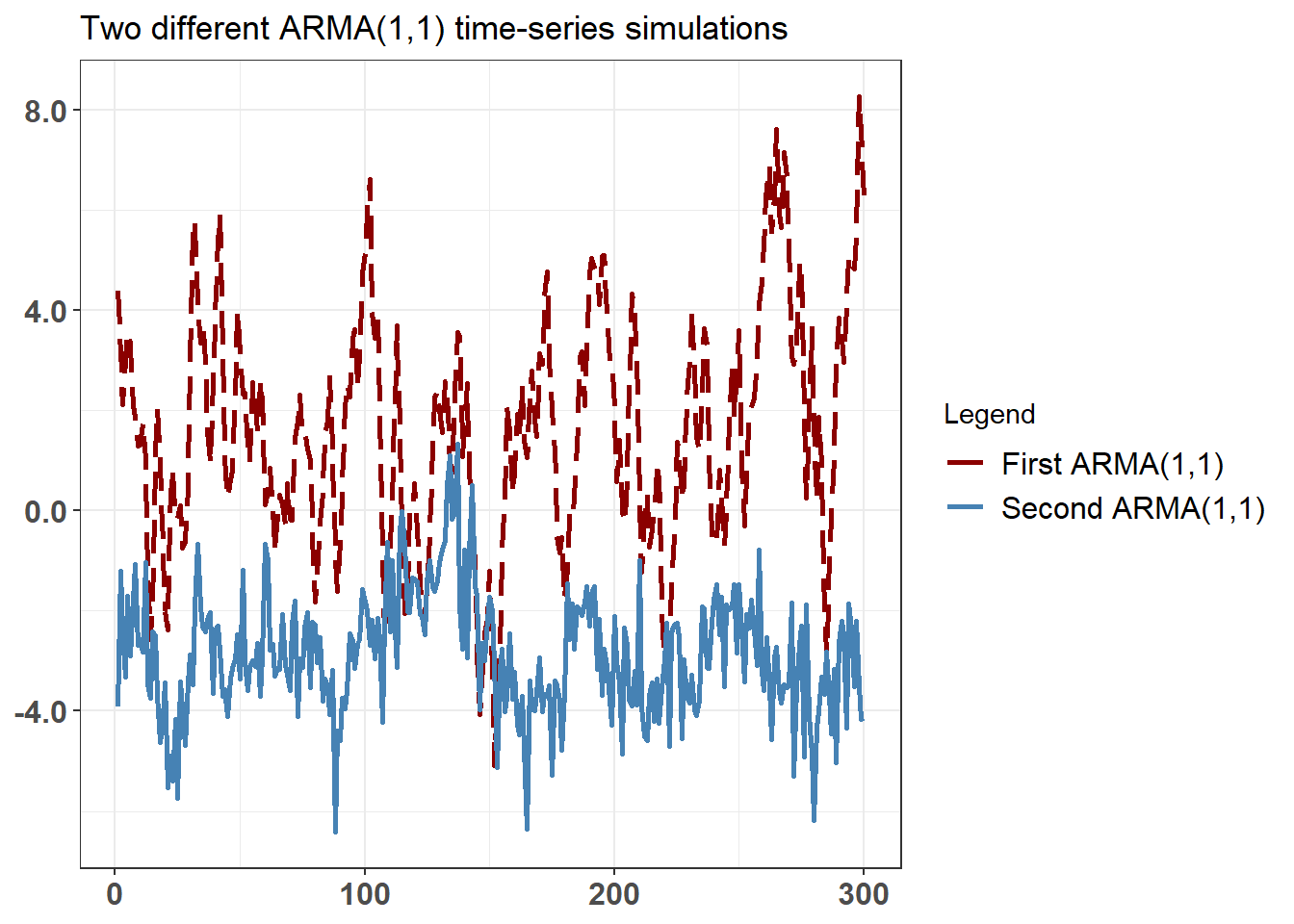
arma_11_1_mulr = arma_11_1_mu/(1 - ar_11_1)
arma_11_2_mulr = arma_11_2_mu/(1 - ar_11_2)
# mu_arma_22 = 10
#ARMA_22 <- arima.sim(model=list(order = c(2, 0, 2), ar = c(0.4, 0.2), ma = c(0.5,0.6)), n = 200, mean = mu_arma_22)
# ts.plot(ARMA_22)
# acf2(ARMA_22)
# mean_arma_22 = mu_arma_22/(1 - 0.4 - 0.2)
acf2(ARMA_11_1)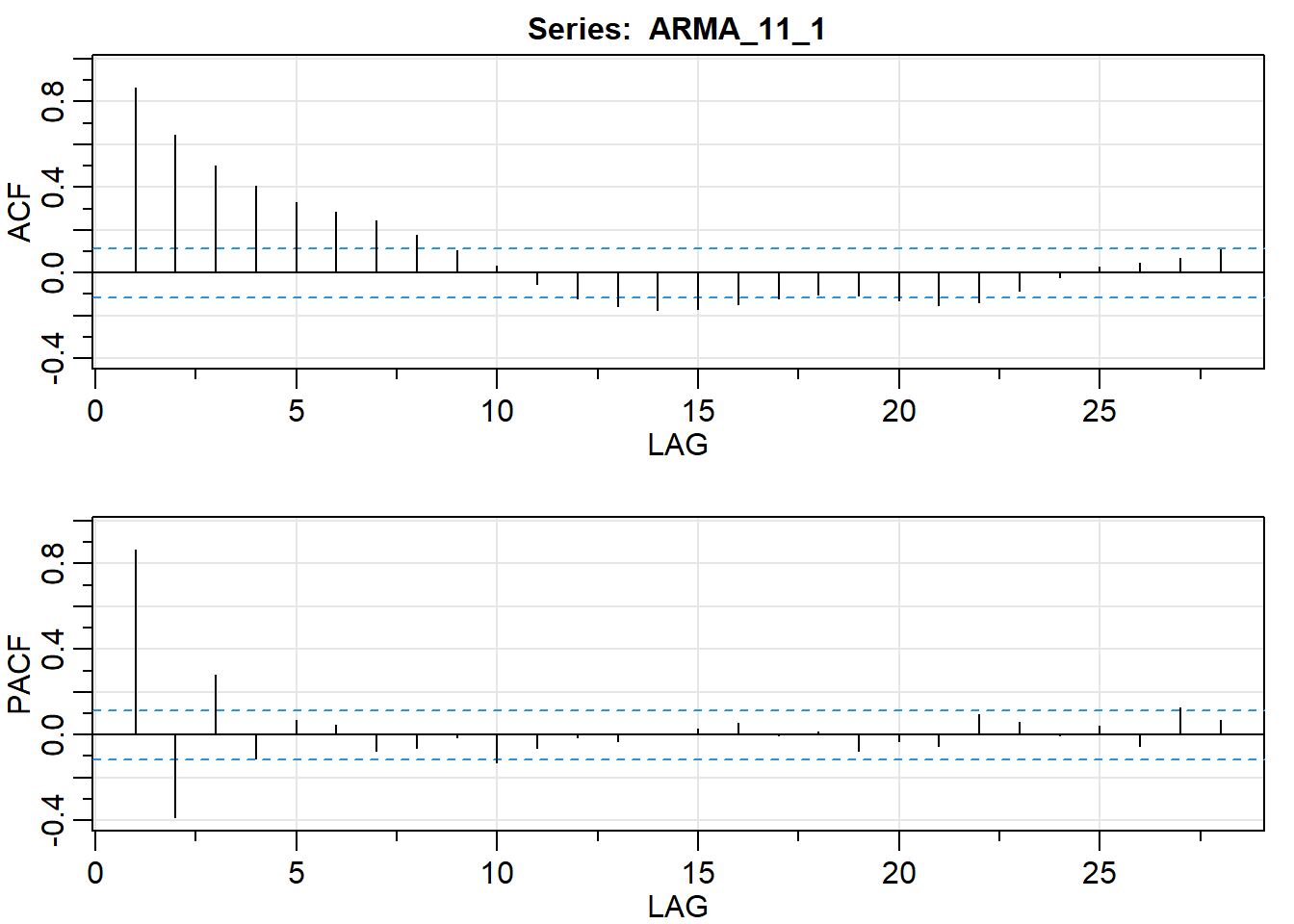
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF 0.86 0.65 0.50 0.40 0.33 0.29 0.24 0.18 0.11 0.03 -0.05 -0.12 -0.16
## PACF 0.86 -0.39 0.28 -0.11 0.07 0.05 -0.07 -0.06 -0.01 -0.13 -0.06 -0.01 -0.03
## [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
## ACF -0.17 -0.17 -0.15 -0.12 -0.10 -0.11 -0.13 -0.15 -0.14 -0.08 -0.02 0.03
## PACF 0.01 0.03 0.06 0.00 0.01 -0.08 -0.03 -0.05 0.10 0.06 0.00 0.04
## [,26] [,27] [,28]
## ACF 0.05 0.07 0.11
## PACF -0.05 0.13 0.07acf2(ARMA_11_2)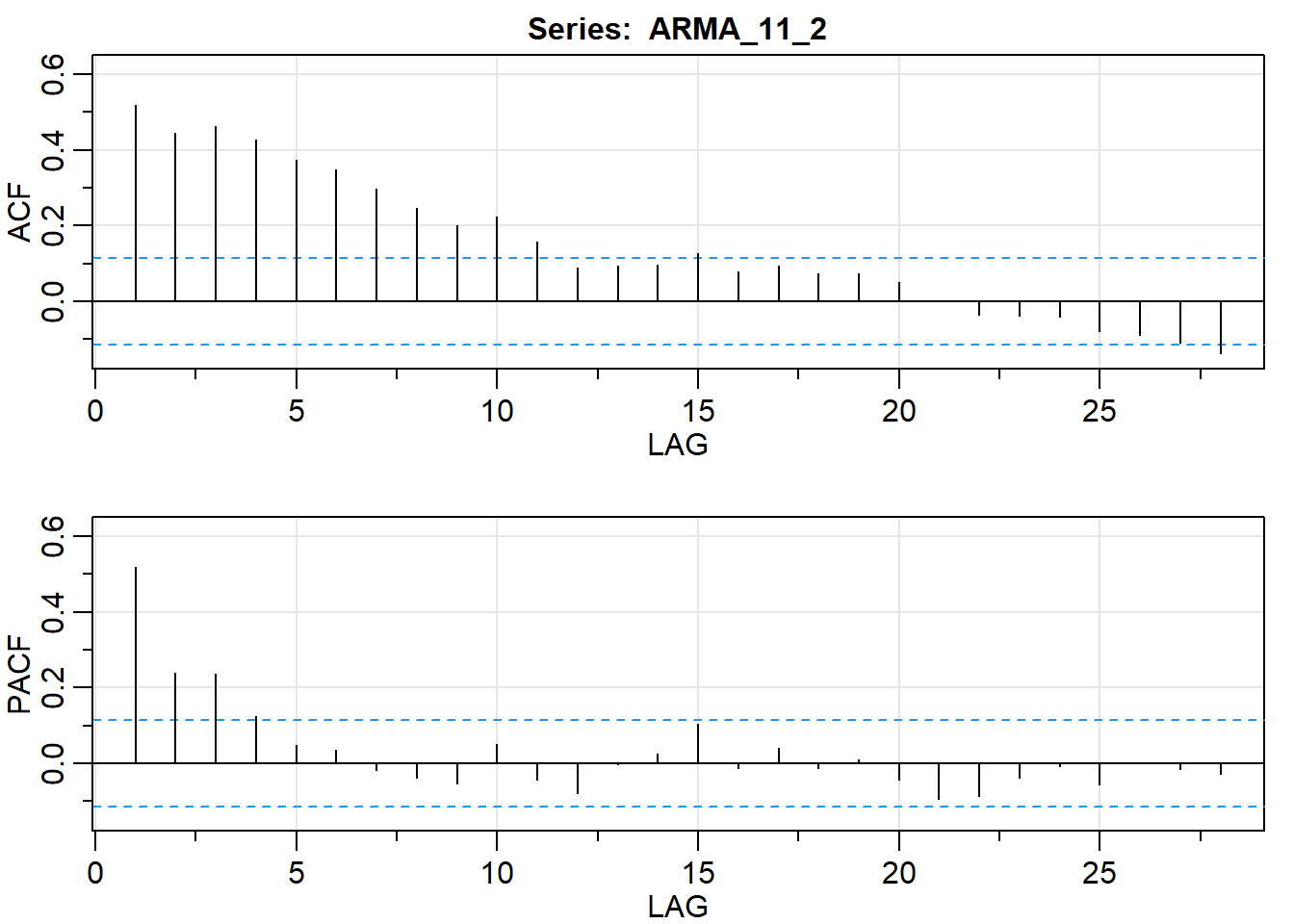
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF 0.52 0.45 0.46 0.43 0.37 0.35 0.30 0.25 0.20 0.22 0.16 0.09 0.09
## PACF 0.52 0.24 0.24 0.12 0.05 0.04 -0.02 -0.04 -0.05 0.05 -0.04 -0.08 0.00
## [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
## ACF 0.10 0.13 0.08 0.09 0.08 0.07 0.05 0.00 -0.04 -0.04 -0.04 -0.08
## PACF 0.03 0.10 -0.01 0.04 -0.01 0.01 -0.04 -0.09 -0.09 -0.04 -0.01 -0.06
## [,26] [,27] [,28]
## ACF -0.09 -0.11 -0.14
## PACF 0.00 -0.01 -0.03