BT Question Set P1-T2-20-24-3: AIC and BIC

Last updated on Oct 21, 2020 10 min read

20.24.3. Eric is a commodity analyst who fit four different candidate AR(p) models to a series of oil prices. For each of the candidate models, he then retrieved the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). The results are displayed below.

.. AIC and BIC values (table below) goes here …

As Eric interprets the results of these criteria (i.e., the AIC and BIC values), which of the following statements is TRUE?

  1. Both criteria (AIC and BIC) favor the AR(1) model
  2. Both criteria (AIC and BIC) favor the AR(2) model
  3. As both criteria are insignificant, any AR(p) model is a bad fit
  4. The criteria disagree and therefore the AIC’s preference should prevail because it prefers fewer lags
library(tidyverse)
library(scales)
library(gridExtra)
library(forecast)
library(tseries)
library(fpp2)
library(gt)
library(astsa)

# 175
set.seed(175)
ar2 <- arima.sim(model=list(order=c(2,0,0),ar = c(1.5,-.75)),n = 500)
ma2 <- arima.sim(model=list(order=c(0,0,2),ma = c(1.5,-.75)),n = 500)

ar1_fit <- sarima(ar2, p = 1, d = 0, q = 0)
## initial  value 1.185288 
## iter   2 value 0.473121
## iter   3 value 0.473113
## iter   4 value 0.473112
## iter   5 value 0.473108
## iter   6 value 0.473099
## iter   7 value 0.473095
## iter   8 value 0.473094
## iter   9 value 0.473092
## iter  10 value 0.473087
## iter  11 value 0.473080
## iter  12 value 0.473076
## iter  13 value 0.473075
## iter  14 value 0.473075
## iter  15 value 0.473075
## iter  16 value 0.473074
## iter  17 value 0.473073
## iter  18 value 0.473073
## iter  19 value 0.473073
## iter  20 value 0.473073
## iter  21 value 0.473072
## iter  22 value 0.473072
## iter  23 value 0.473072
## iter  24 value 0.473072
## iter  25 value 0.473072
## iter  26 value 0.473072
## iter  27 value 0.473072
## iter  27 value 0.473072
## iter  27 value 0.473072
## final  value 0.473072 
## converged
## initial  value 0.475632 
## iter   2 value 0.475627
## iter   3 value 0.475615
## iter   4 value 0.475613
## iter   5 value 0.475597
## iter   6 value 0.475583
## iter   7 value 0.475579
## iter   8 value 0.475574
## iter   9 value 0.475573
## iter  10 value 0.475570
## iter  11 value 0.475569
## iter  12 value 0.475569
## iter  13 value 0.475569
## iter  13 value 0.475569
## iter  13 value 0.475569
## final  value 0.475569 
## converged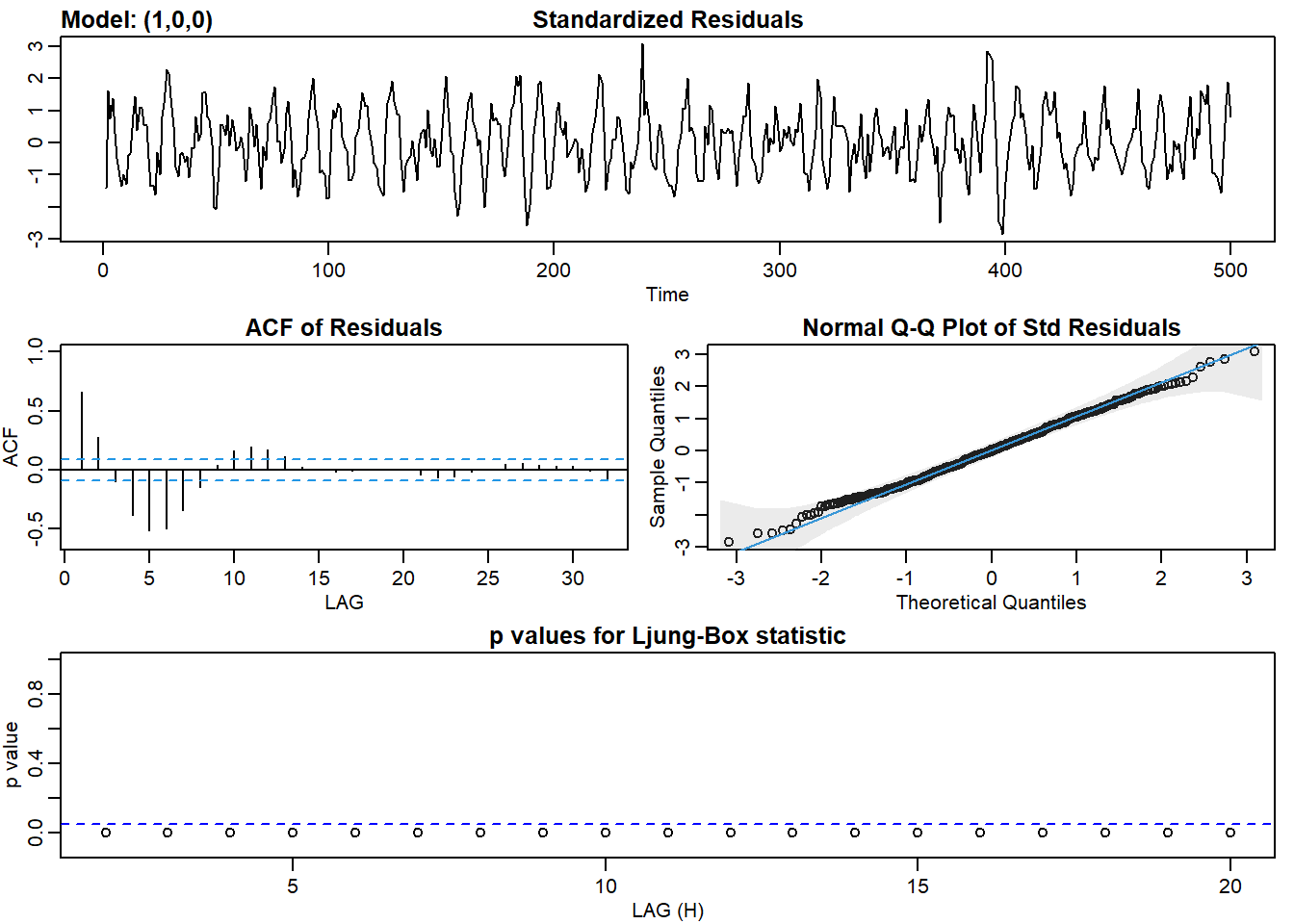

ar2_fit <- sarima(ar2, p = 2, d = 0, q = 0)
## initial  value 1.186082 
## iter   2 value 1.063752
## iter   3 value 0.611728
## iter   4 value 0.360300
## iter   5 value 0.180452
## iter   6 value 0.026222
## iter   7 value 0.023222
## iter   8 value 0.022348
## iter   9 value 0.022310
## iter  10 value 0.022284
## iter  11 value 0.022258
## iter  12 value 0.022258
## iter  13 value 0.022258
## iter  14 value 0.022258
## iter  15 value 0.022258
## iter  16 value 0.022258
## iter  17 value 0.022258
## iter  17 value 0.022258
## iter  17 value 0.022258
## final  value 0.022258 
## converged
## initial  value 0.028108 
## iter   2 value 0.028095
## iter   3 value 0.028087
## iter   4 value 0.028086
## iter   5 value 0.028086
## iter   6 value 0.028085
## iter   7 value 0.028085
## iter   8 value 0.028085
## iter   8 value 0.028085
## final  value 0.028085 
## converged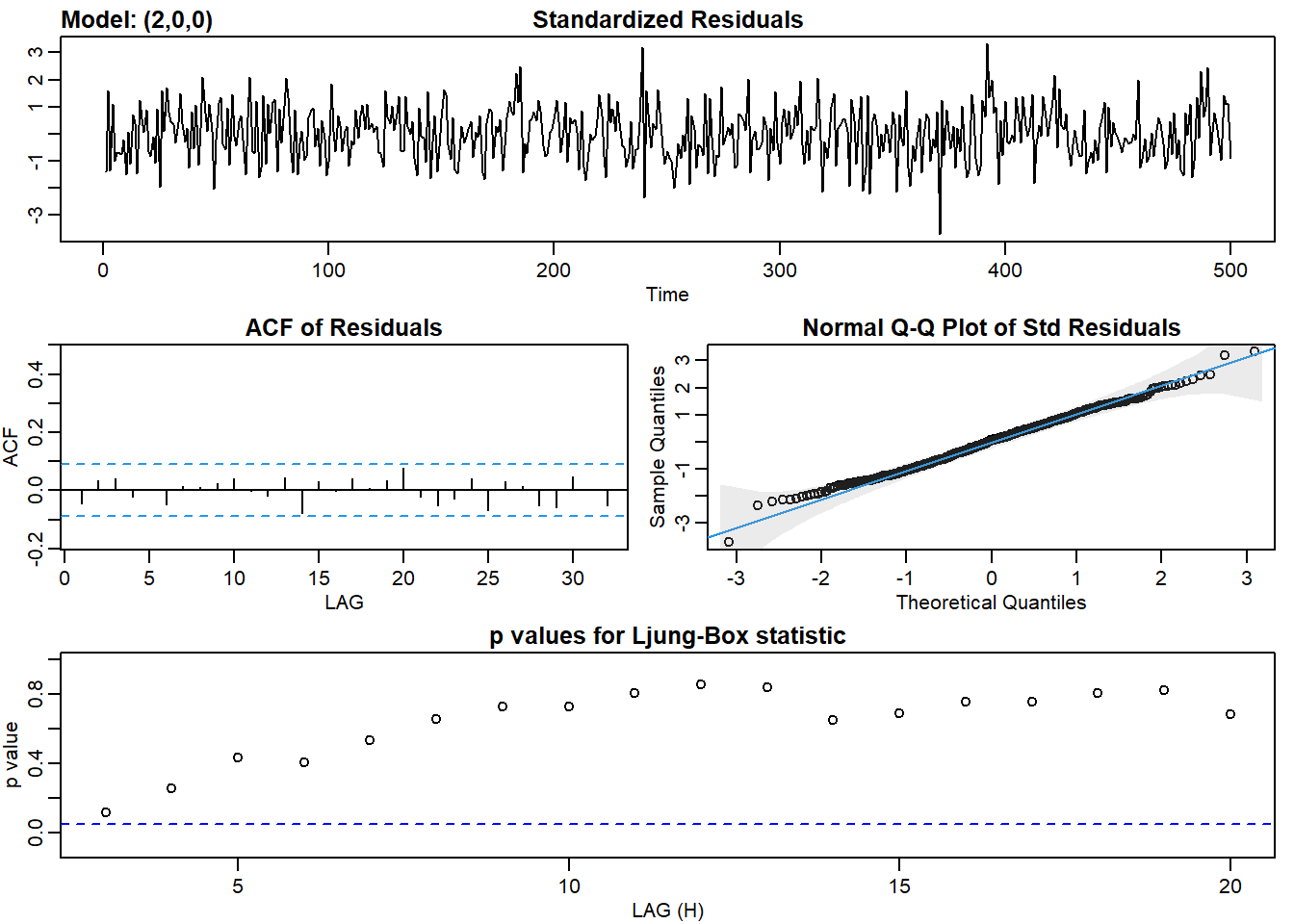

ar3_fit <- sarima(ar2, p = 3, d = 0, q = 0)
## initial  value 1.187086 
## iter   2 value 0.966297
## iter   3 value 0.720122
## iter   4 value 0.651535
## iter   5 value 0.270365
## iter   6 value 0.157749
## iter   7 value 0.106223
## iter   8 value 0.068752
## iter   9 value 0.027592
## iter  10 value 0.020453
## iter  11 value 0.020449
## iter  12 value 0.020445
## iter  13 value 0.020430
## iter  14 value 0.020418
## iter  15 value 0.020418
## iter  16 value 0.020418
## iter  17 value 0.020418
## iter  18 value 0.020418
## iter  19 value 0.020418
## iter  20 value 0.020418
## iter  20 value 0.020418
## iter  20 value 0.020418
## final  value 0.020418 
## converged
## initial  value 0.027093 
## iter   2 value 0.027090
## iter   3 value 0.027084
## iter   4 value 0.027079
## iter   5 value 0.027079
## iter   6 value 0.027078
## iter   7 value 0.027078
## iter   8 value 0.027078
## iter   8 value 0.027078
## iter   8 value 0.027078
## final  value 0.027078 
## converged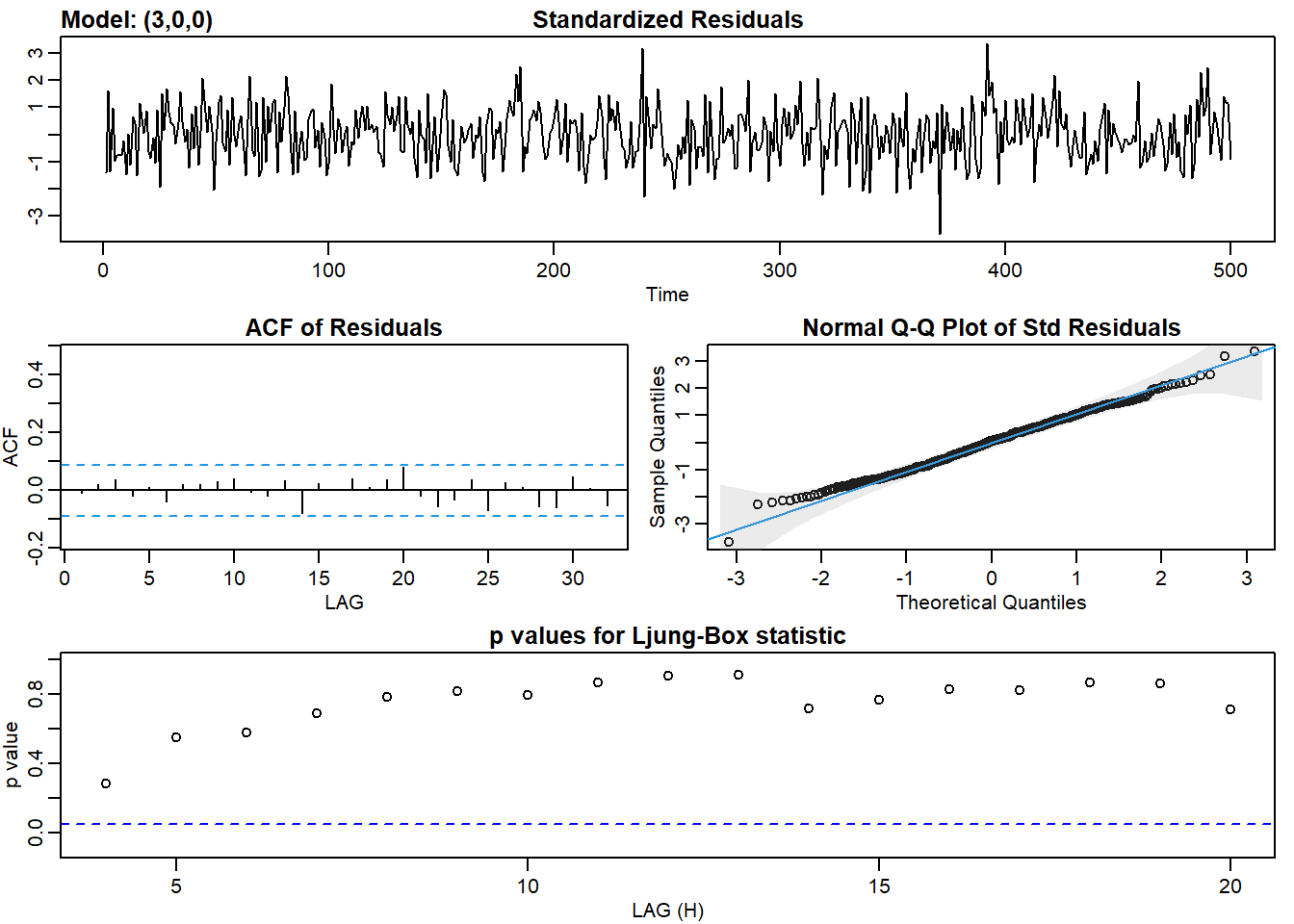

ar4_fit <- sarima(ar2, p = 4, d = 0, q = 0)
## initial  value 1.187677 
## iter   2 value 1.182760
## iter   3 value 0.389837
## iter   4 value 0.312734
## iter   5 value 0.257361
## iter   6 value 0.134886
## iter   7 value 0.042493
## iter   8 value 0.035479
## iter   9 value 0.028843
## iter  10 value 0.020356
## iter  11 value 0.020308
## iter  12 value 0.020305
## iter  13 value 0.020305
## iter  14 value 0.020305
## iter  15 value 0.020304
## iter  16 value 0.020304
## iter  17 value 0.020304
## iter  18 value 0.020304
## iter  19 value 0.020304
## iter  20 value 0.020304
## iter  21 value 0.020304
## iter  22 value 0.020304
## iter  22 value 0.020304
## iter  22 value 0.020304
## final  value 0.020304 
## converged
## initial  value 0.026957 
## iter   2 value 0.026941
## iter   3 value 0.026940
## iter   4 value 0.026938
## iter   5 value 0.026937
## iter   6 value 0.026936
## iter   7 value 0.026936
## iter   8 value 0.026936
## iter   9 value 0.026936
## iter   9 value 0.026936
## iter   9 value 0.026936
## final  value 0.026936 
## converged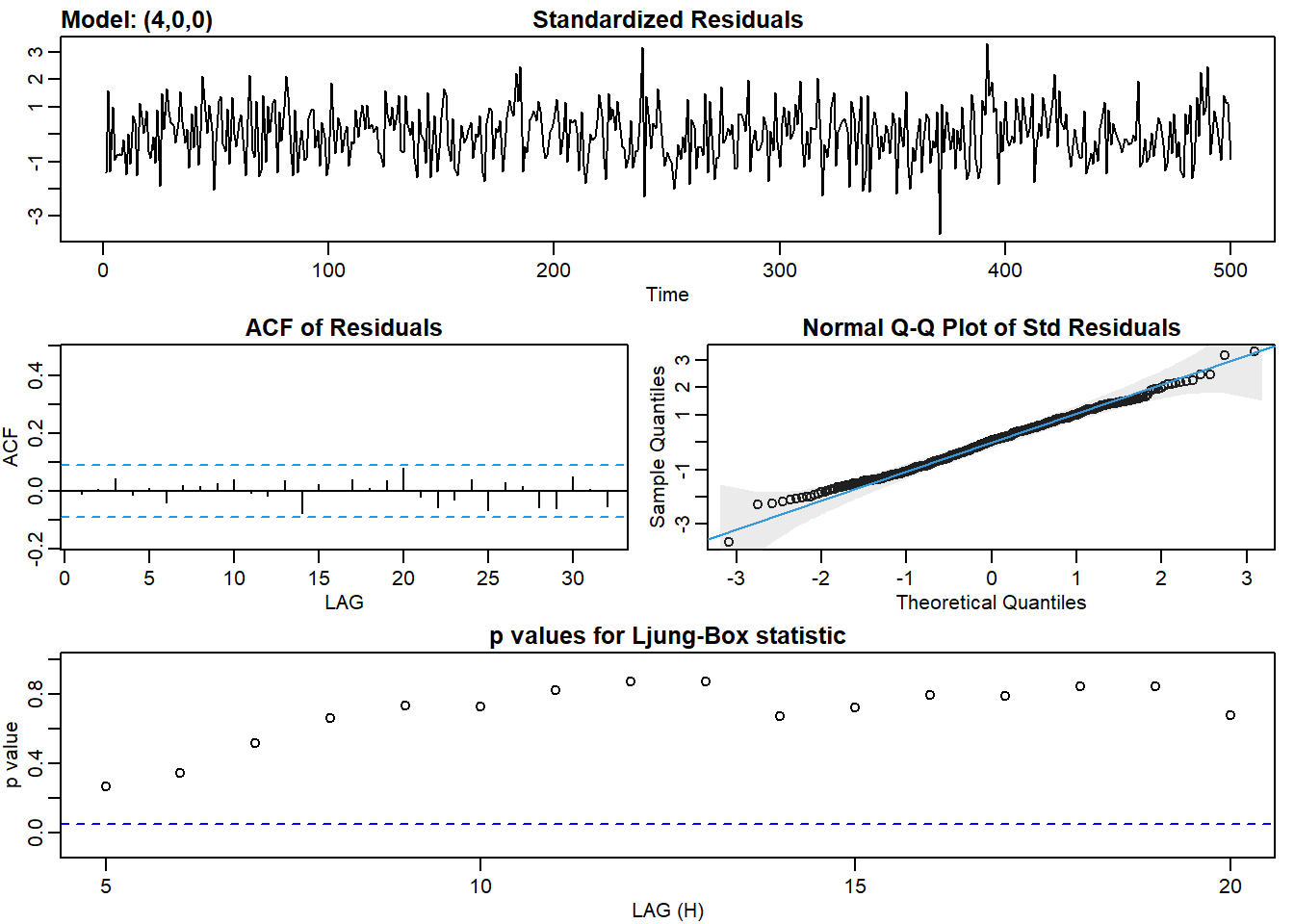

ma1_fit <- sarima(ma2, p = 0, d = 0, q = 1)
## initial  value 0.620720 
## iter   2 value 0.616967
## iter   3 value 0.616503
## iter   4 value 0.616503
## iter   4 value 0.616503
## iter   4 value 0.616503
## final  value 0.616503 
## converged
## initial  value 0.616515 
## iter   2 value 0.616515
## iter   2 value 0.616515
## iter   2 value 0.616515
## final  value 0.616515 
## converged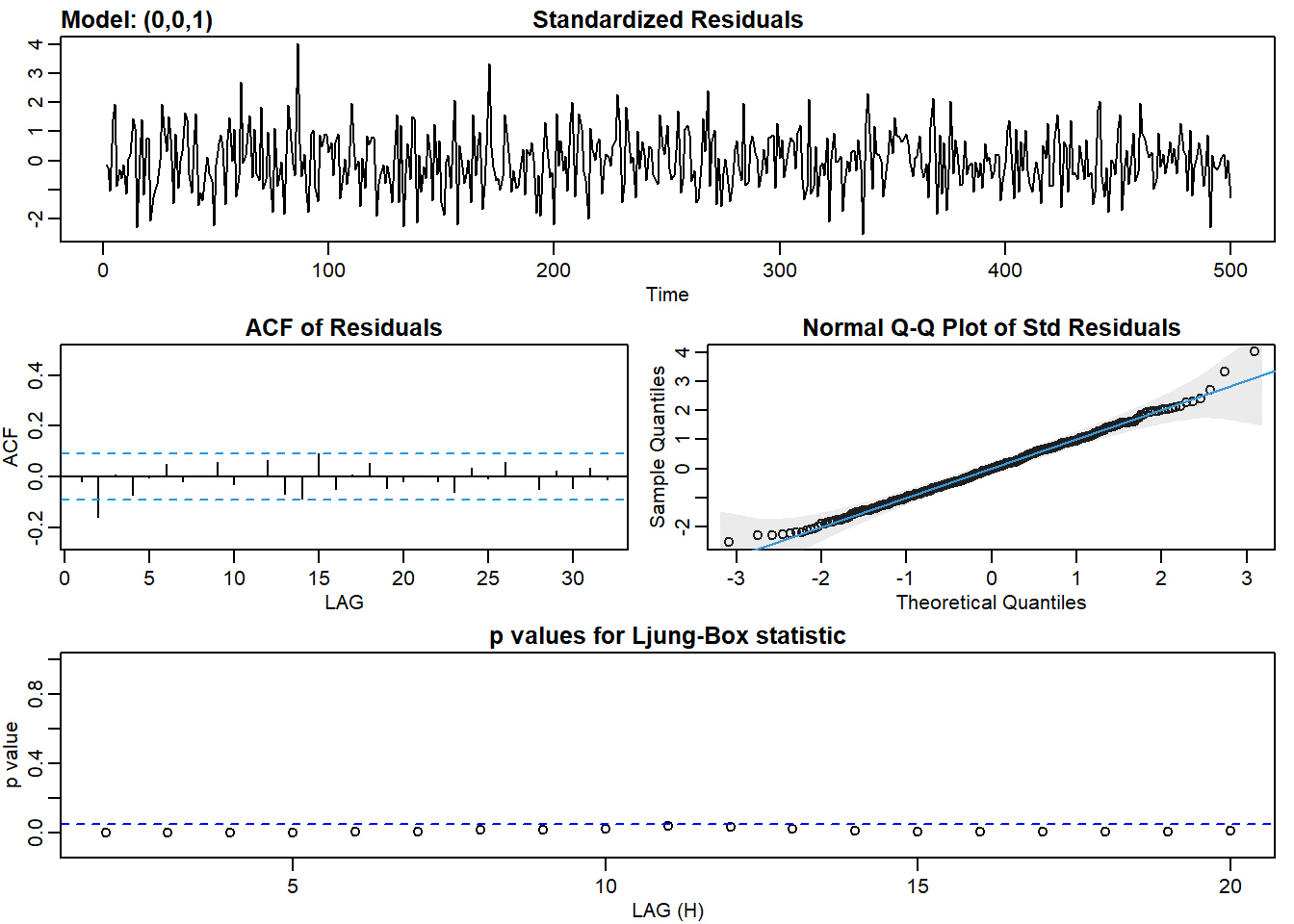

ma2_fit <- sarima(ma2, p = 0, d = 0, q = 2)
## initial  value 0.620720 
## iter   2 value 0.601563
## iter   3 value 0.601097
## iter   4 value 0.601053
## iter   5 value 0.601053
## iter   5 value 0.601053
## iter   5 value 0.601053
## final  value 0.601053 
## converged
## initial  value 0.601132 
## iter   2 value 0.601132
## iter   2 value 0.601132
## iter   2 value 0.601132
## final  value 0.601132 
## converged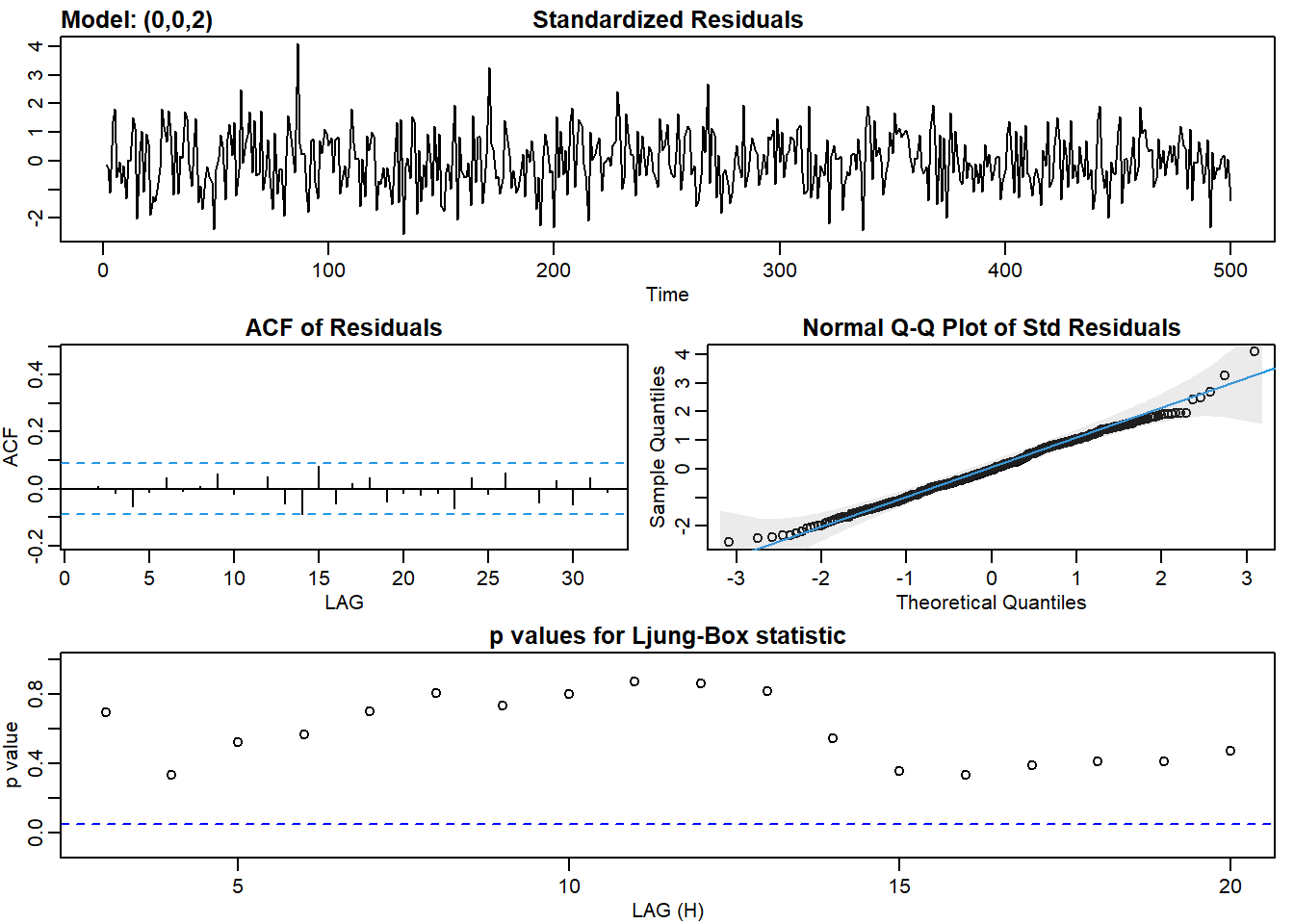

ma3_fit <- sarima(ma2, p = 0, d = 0, q = 3)
## initial  value 0.620720 
## iter   2 value 0.601584
## iter   3 value 0.601080
## iter   4 value 0.600978
## iter   5 value 0.600977
## iter   5 value 0.600977
## iter   5 value 0.600977
## final  value 0.600977 
## converged
## initial  value 0.601058 
## iter   2 value 0.601058
## iter   3 value 0.601058
## iter   3 value 0.601058
## iter   3 value 0.601058
## final  value 0.601058 
## converged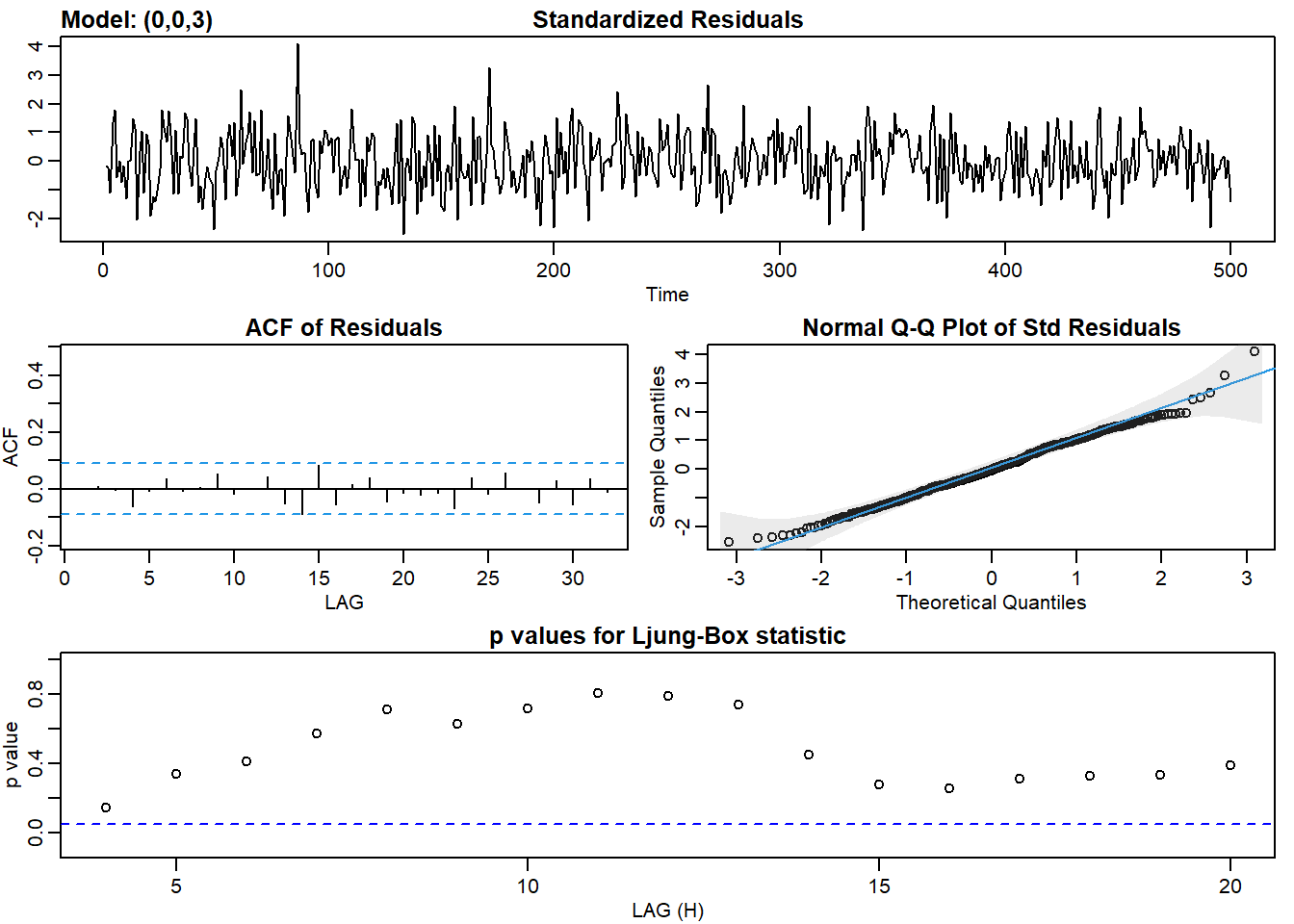

ma4_fit <- sarima(ma2, p = 0, d = 0, q = 4)
## initial  value 0.620720 
## iter   2 value 0.599626
## iter   3 value 0.599377
## iter   4 value 0.599342
## iter   5 value 0.599340
## iter   6 value 0.599340
## iter   7 value 0.599340
## iter   7 value 0.599340
## iter   7 value 0.599340
## final  value 0.599340 
## converged
## initial  value 0.599424 
## iter   2 value 0.599424
## iter   3 value 0.599424
## iter   3 value 0.599424
## iter   3 value 0.599424
## final  value 0.599424 
## converged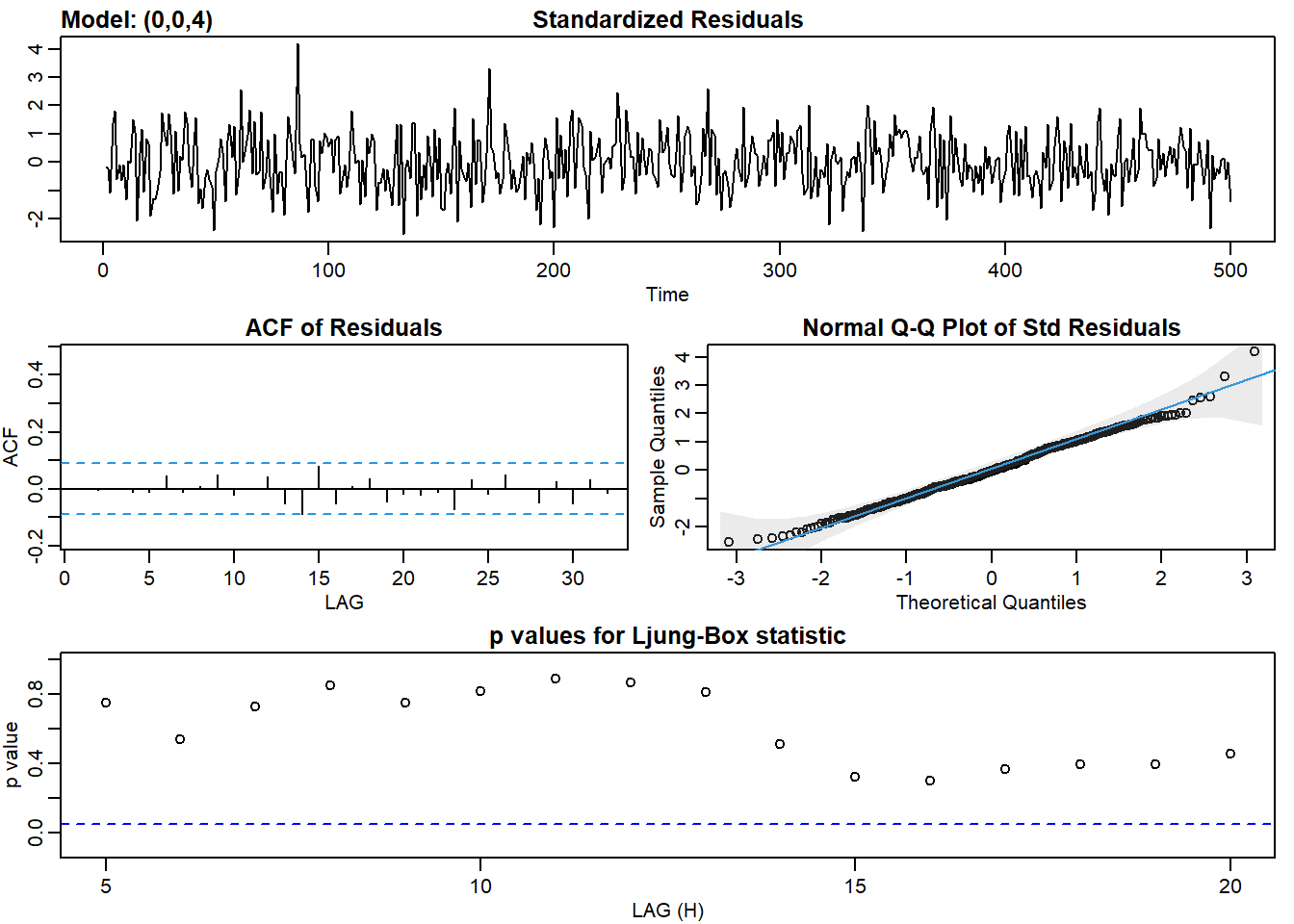

print("AIC")
## [1] "AIC"
ar1_fit$AIC
## [1] 3.801016
ar2_fit$AIC
## [1] 2.910047
ar3_fit$AIC
## [1] 2.912034
ar4_fit$AIC
## [1] 2.915749
print("BIC")
## [1] "BIC"
ar1_fit$BIC
## [1] 3.826304
ar2_fit$BIC
## [1] 2.943764
ar3_fit$BIC
## [1] 2.95418
ar4_fit$BIC
## [1] 2.966324
AIC_ar2 <- c(ar1_fit$AIC, ar2_fit$AIC, ar3_fit$AIC, ar4_fit$AIC)
BIC_ar2 <- c(ar1_fit$BIC, ar2_fit$BIC, ar3_fit$BIC, ar4_fit$BIC)
AIC_BIC_ar2 <- cbind(AIC_ar2, BIC_ar2) %>% data.frame()
models <- c("AR(1)", "AR(2)", "AR(3)", "AR(4)")
models_AIC_BIC <- cbind(models, AIC_BIC_ar2)

models_AIC_BIC_gt <- gt(models_AIC_BIC)

models_AIC_BIC_gt <- 
  models_AIC_BIC_gt %>% 
  tab_options(
    table.font.size = 14
  ) %>% tab_style(
    style = cell_text(weight = "bold"),
    locations = cells_body()
  # ) %>% tab_style(
  #  style = cell_text(color = "cadetblue"),
  #  locations = cells_column_labels(
  #    columns = vars(model, 'h (lags)', statistic, 'p-value')
  #  )
  ) %>% tab_header(
    title = md("**AIC and BIC values**"),
    subtitle = "Four candidate models: AR(1) ... AR(4)"
  ) %>% fmt_number(
    columns = vars(AIC_ar2, BIC_ar2),
    decimals = 5
  ) %>% tab_source_note(
    source_note = md("AIC = Akaike information criterion")
  ) %>% tab_source_note(
    source_note = md("BIC = Bayesian information criterion")
  # ) %>% cols_width(
  #  vars(model) ~ px(70),
  #  vars(statistic, 'p-value') ~ px(90)
  ) %>% cols_label (
    models = md("**model**"),
    AIC_ar2 = md("**AIC**"),
    BIC_ar2 = md("**BIC**")
  ) %>% tab_options(
    heading.title.font.size = 16,
    heading.subtitle.font.size = 14
  )

models_AIC_BIC_gt
AIC and BIC values
Four candidate models: AR(1) ... AR(4)
model AIC BIC
AR(1) 3.80102 3.82630
AR(2) 2.91005 2.94376
AR(3) 2.91203 2.95418
AR(4) 2.91575 2.96632
AIC = Akaike information criterion
BIC = Bayesian information criterion
R
David Harper
David Harper
Founder & CEO of Bionic Turtle

I teach financial risk and enjoy learning data science

Related